p.100
절사평균(trimmed mean)은 평균의 장점과 중앙값의 장점을 모두 갖는 대푯값입니다. 절사평균을 가장 많이 활용하는 분야는 심판의 채점으로 등수를 정하는 운동경기입니다. 체조, 다이빙, 그리고 피겨스케이팅에서 심판으로 주관적인 편견을 배제하고 보완하기 위해 제일 높은 점수와 제일 낮은 점수를 제외(중앙값의 장점)한 나머지 심판들의 점수 평균(평균의 장점)으로 판정하는데 이를 절사평균이라 합니다.
절사평균을 계산하려면 절사 비율(%)을 결정해야 합니다. 절사 비율은 전체 데이터의 개수에 대해 몇 %의 데이터(상위+하위)를 배제할 것인가로 결정합니다. 만약 10개의 데이터에 대해 가장 낮은 점수와 가장 높은 점수 각각 1개씩 2개를 배제한다면 절사 비율은 10%(1/10)입니다. 따라서 10개의 데이터에 대해 10% 절사평균은 데이터를 순서대로 나열했을 때 가운데 위치하는 8개의 평균으로 계산합니다.
p.101
심슨의 패러독스
평균은 데이터의 대푯값으로 사용할 만큼 통계에서 중요한 역할을 합니다. 그런데 이런 평균이 제시하는 숫자에 대해 오류에 빠지기 쉽습니다. 이러한 오류는 여러 그룹의 자료를 합하여 계산한 결과와 그룹별로 구분해서 얻은 결과가 다를 경우에 발생하는데 이를 '심슨의 패러독스'라 합니다.
어느 대학의 취업률 자료를 분석한 결과 남학생의 취업률은 66.7%이고, 여학생의 취업률은 50%로 여학생의 취업률이 낮아 보이지만, 인문계와 자연계로 구분하여 취업률을 조사하면 여학생의 취업률이 높은 것으로 나타납니다.
| 전체 | 남학생 | 여학생 |
| 대상자 | 1,500 | 1,000 |
| 취업자 | 1,000 | 500 |
| 취업률 | 66.7% | 50% |
| 인문계 | 남학생 | 여학생 |
| 대상자 | 200 | 800 |
| 취업자 | 50 | 350 |
| 취업률 | 25% | 44% |
| 자연계 | 남학생 | 여학생 |
| 지원자 | 1,300 | 200 |
| 취업자 | 950 | 150 |
| 취업률 | 73% | 75% |
이런 오류를 보완하려는 시도는 여러 곳에서 볼 수 있으며, 특히 우리가 쉽게 접하는 야구 경기의 중계방송에서 흔하게 볼 수 있습니다. 과거의 방송에서는 타자의 타율을 가장 중요하게 평가했으며, 그 외에 홈런 수, 도루 수 등을 주로 제공했지만, 근래에 들어 다양하고 구체적으로 계산된 추가적인 정보를 제공하고 있습니다.
예를 들어, 상대 투수에 대한 타율, 상대 팀에 대한 타율, 우/좌타자에 대한 타율을 비롯하여 우/좌투수에 대한 타격 분포도, 우/좌타자에 대한 투구 분포도 등을 제공하고 있으며, 타율 외에도 출루율이나 장타율 등의 정보도 쉽게 볼 수 있습니다.
p.106~107
데이터의 비대칭도
대푯값과 산포도를 계산하면 데이터의 특성을 요약할 수 있지만, 분포의 모양에 대해 좀 더 구체적인 특징을 나타내기 위해서 사용하는 척도로써 왜도(skewness)와 첨도(kurtosis)가 있습니다.
왜도는 분포의 모양이 대푯값(예를 들어 평균)을 중심으로 좌우의 모양이 대칭적인가 아닌가를 측정하는데, 이를 통해 데이터가 한쪽(오른쪽 또는 왼쪽)으로 얼마나 치우쳐져 있는가를 나타냅니다.
첨도는 분포가 대푯값을 중심으로 얼마나 모여 있는가를 나타내는 척도인데 나중에 설명할 정규분포(첨도 = 3)를 기준으로 비교합니다.
p.118
- 확률분포(probability distribution) : 실험이나 관찰을 통해 발생 가능한 모든 값과 그 값이 나타날 가능성, 즉 확률을 도표나 그래프로 표시한 것
- 확률변수(random variable) : 실험이나 관찰의 결괏값을 실수로 대응시키는 함수
다른 말로 설명하면 확률변수는 일정한 확률로 나타나는(발생하는) 사건에 대해 숫자를 부여한 변수라고 할 수 있습니다. 따라서 확률분포는 확률변수가 취할 수 있는 모든 값에 대해 각각의 확률을 대응시킨 것입니다.
[한 개의 동전을 던지는 실험]
| 사건 | 확률변수(X) | 확률변수의 확률 |
| 뒷면 | X = 0 | P(X=0) = 0.5 |
| 앞면 | X = 1 | P(X=1) = 0.5 |
[두 개의 동전을 던지는 실험]
| 사건 | 확률변수(X) | 확률변수의 확률 |
| 뒷면, 뒷면 | X = 0 | P(X = 0) = 0.25 |
| 뒷면, 앞면 | X = 1 | P(X = 1) = 0.5 |
| 앞면, 뒷면 | ||
| 앞면, 앞면 | X = 2 | P(X = 2) = 0.25 |
p.124
파이썬에서 확률분포의 확률 계산은 모듈 scipy.stats를 사용하고 특히 이항확률분포와 관련된 확률은 stats.scipy.binom을 사용합니다. 이항확률분포의 확률은 pmf를 이용하는데 pmf는 probability mass function(확률질량함수)의 약자로 이산확률분포에 대한 확률을 계산할 때 사용하는 함수입니다.
| 함수 | 함수 인자 | 반환값 |
| scipy.stats.binom.stats(n, p) | - n : 시행 횟수 - p : 성공할 확률 |
해당 이산확률분포의 평균과 분포 계산 |
| scipy.stats.binom.pmf(x, n, p) | - x : 확률변수(0~n) - n : 시행 횟수 - p : 성공할 확률 |
확률변수 X에 대한 확률 계산 |
p.125
확률질량함수는 특정 확률변수에 대한 확률을 계산하지만, 특정 확률변수의 범위나 특정 확률변수보다 같거나 작을 확률을 계산할 때는 누적분포함수(cdf, cumulative distribution function)를 이용합니다. P(X <= 3)은 다음과 같이 계산합니다.
P(X <= 3) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
| 함수 | 함수 인자 | 반환값 |
| scipy.stats.binom.cdf(r, n, p) | - r : 확률변수( 0 ~n) - n : 시행횟수 - p : 성공할 확률 |
확률변수 r에 대한 누적확률 계산 |
p.126
이항확률분포에 대한 누적분포함수의 역함수
동전을 100번 던졌을 경우 앞면이 나타난 횟수를 X라 할 때, P(X <= k) = 0.95를 만족하는 확률 변수 k를 계산하시오.
누적분포함수 문제에서는 확률변수가 주어진 상태에서 확률을 계산했지만, 이 경우에는 거꾸로 확률이 주어진 상태에서 확률변수를 계산하는 문제입니다. 즉, 확률변수 k보다 같거나 작을 누적확률이 0.95를 만족하는 k를 계산해야 하는데, 이때 누적분포함수의 역함수(inverse cummulative distribution function)을 이용하며, 파이썬에서는 ppf(percent point function)로 계산합니다.
| 함수 | 함수 인자 | 반환 값 |
| scipy.stats.binom.ppf(q, n, p) | - q : percent point - n : 시행 횟수 - p : 성공 확률 |
percent point q를 만족하는 확률변수 계산 |
p.130
| 함수 | 함수 인자 | 반환값 |
| scipy.stats.norm.pdf(x, m, s) | - x : 확률변수 - m : 평균 - s : 표준편차 |
확률변수 X에 대한 확률밀도함수 계산 |
p.133
T 점수(T-Score)란?
원점수에 대한 표준점수로 Z 점수와 T점수를 많이 사용합니다. Z점수는 앞과 같이 음수 값을 갖고 소수점을 포함하므로 이러한 단점을 없애기 위해 Z 점수에 대해 다음과 같은 변환을 한 표준점수입니다.
T = 10Z + 50
Z점수는 N(0, 1)의 정규분포를 따르므로 T = 10Z + 50에 의해 T점수는 평균이 50, 표준편차가 10인 정규분포를 따릅니다. Z점수가 -3 <= Z <= 3에 해당한다면 T점수는 20 <= T <= 80의 범위를 갖게 되므로 일반적인 100점 만점의 단위로 사용할 수 있으며, 여러 다른 집단 간의 점수를 비교하거나 통합할 때 사용합니다.
p.137
파이썬에서 정규분포나 표준정규분포의 확률은 모두 동일한 함수로 계산하며, 특정 구간에 대한 확률을 계산하기 위해서 cdf(누적분포함수)를 이용하여 다음과 같이 계산합니다.
| 함수 | 함수 인자 | 반환 값 |
| scipy.stats.norm.cdf(x, m, s) | - x : 확률변수 - m : 평균 - s : 표준편차 |
확률변수 X에 대한 누적확률 계산 |
p.139
정규분포에 대한 누적분포함수의 역함수
파이썬에서 누적분포함수의 역함수(inverse cumulative distribution function)는 ppf(percent point function)로 계산합니다.
| 함수 | 함수 인자 | 반환 값 |
| scipy.stats.norm.ppf(q, m, s) | - q : percent point - m : 평균 - s : 표준편차 |
percent point q르르 만족하는 확률변수 계산 |
p.140
데이터가 정규분포를 따르는지 그래프로 확인하는 방법
QQ plot(Quantile Quantile plot)은 수집한 데이터가 특정한 확률분포를 따르는가를 분석하는 데 사용하며, 만약 데이터가 특정한 확률분포를 따른다면 직선 형태로 나타납니다. 일반적으로 데이터가 정규분포를 따르는가를 확인할 때 사용합니다. 파이썬에서 QQ plot은 함수 qqplot()을 사용합니다.
| 함수 | 함수 인자 |
| statsmodels.graphics.gofplots.qqplot(data, dist, line) | - data : 데이터 배열 - dist : 연속확률분포 norm (default) - line : 45 (45도 라인) |
p.148
비유하자면 냄비에 들어 있는 국물 전체를 모집단(population)이라 할 수 있고, 국물로부터 뜬 한 숟가락의 국물을 표본(ssample)이라 할 수 있습니다. 국물(모집단)에 대해서 한 숟가락의 양(표본)으로 얻은 정보만으로도 국물 전체(모집단)의 특징인 맛과 간을 파악할 수 있습니다.
p.149
표본으로부터 추측하려는 모집단의 특성 중 가장 중요한 것은 표본의 평균과 표준편차입니다. 모집단의 평균(mu)와 표준편차(sigma)를 모수(parameter)라 하고, 표본으로부터 얻은 평균(X_bar)과 표준편차(S)를 표본 통계량(sample statistic)이라 합니다.
p.152
중심극한정리(CLT)
X가 임의의 모집단으로부터 추출한 표본이더라도, 표본의 크기 n이 충분히 크다면 모집단 분포와 관계없이 표본평균 X_bar에 대한 확률분포는 정규분포, 즉 X_bar ~ N (mu, sigma^2 / n)을 따른다.
또한, 표본평균 X_bar가 정규분포를 따르므로 이에 대한 표준화 Z = (X_bar - mu) / (sigma / sqrt(n))의 분포는 표준정ㄱㅎ분포 N(0, 1)을 따른다.
p.153
모집단 분산 sigma^2을 모르고 표본의 크기 n이 작다면 표본평균 X_bar에 대한 확률분포는 정규분포를 따르지 않고, t분포를 따릅니다.
표본의 표준편차 S =
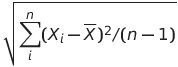
에 대해 t = ( X_bar - mu ) / (S / sqrt(n))라 한다면, t는 자유도 (n - 1)인 t분포, 즉 t_(n-1)을 따르며, 자유도에 따라 분포의 모양이 달라집니다.
자유도가 작을수록 분포의 모양이 납작해지고, 자유도가 증가할수록 표준정규분포와 비슷해집니다.
p.154
t분포의 확률밀도함수는 함수 scipy.stats.t.pdf()를 이용하여 다음과 같이 계산합니다.
| 함수 | 함수 인자 | 반환 값 |
| scipy.stats.t.pdf(x, df) | - x : 확률변수 - df : 자유도 |
확률변수 x에 대한 확률밀도 계산 |
p.155
t분포의 누적분포 함수 (cumulative distribution function) 구하는 방법
| 함수 | 함수 인자 | 반환 값 |
| scipy.stats.t.cdf(t, df) | - t : 확률변수 - df : 자유도 |
확률변수 t에 대한 누적 확률 계산 |
p.155
t분포에 대한 누적분포함수의 역함수
| 함수 | 함수 인자 | 반환 값 |
| scipy.stats.t.ppf(q, df) | - q : percent point - df : 자유도 |
percent point q 를 만족하는 확률변수 계산 |
p.161
좋은 추정량의 선택 기준
- 불편성 : 불편성(unbiasedness)는 편의(biased)가 없다는 뜻으로 추정량의 기댓값이 모수와 같으면 불편성을 만족하는 것이고 이러한 추정량을 불편 추정량이라 합니다. 불편 추정량(unbiased estimator)으로 표본평균(X_bar)과 표본분산(S^2)을 들 수 있습니다.
- 효율성 : 추정량이 불편성을 만족한다고 하더라도 분산이 크다면 편의가 있는 추정량보다 더 낫다고 할 수 없습니다. 효율성(efficiency)은 추정량 중에서 분산이 작은 추정량이 갖는 성질을 의미합니다.
- 일치성 : 일치성(consistency)은 표본의 크기가 증가할수록 추정량이 모수에 일치함을 의미합니다. 표본평균은 표본의 크기가 커질수록 모집단 평균과 같아지는 일치성의 성질을 만족합니다.
p.163
표본평균 X_bar는 표본에 따라 달라지며, 표본평균 X_bar가 달라진다는 것은 동일한 크기의 신뢰수준을 사용하더라도 표본에 따라 추정한 L과 U가 달라질 수 있음을 의미합니다. 따라서 P(L <= mu <= U) = 0.95를 해석할 때 모집단 평균 mu가 L과 U 사이에 있을 확률이 95%가 된다기보다 추정된 구간 L과 U가 모집단 평균 mu를 포함하게 될 것이라는 믿음의 정도(신뢰성의 수준)가 95%가 된다는 의미로 해석합니다.
p.165
구간추정에서 표본평균 X_bar의 표본분포
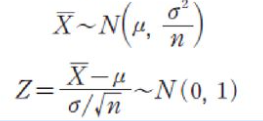
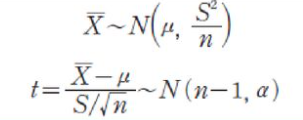
p.175
| 함수 | 함수 인자 |
| scipy.stats.t.interval(alpha, df, loc, scale) | - alpha : 신뢰수준 - df : 자유도 - loc : 표본평균 - scale : 표준오차 |
p.182
고전적 가설검정은 검정이 이루어지기 전에 오로지 유의수준에 의해서 귀무가설을 기각할 것인가 채택할 것인가의 기준이 정해지므로 유의수준의 크기를 어떻게 정하느냐에 따라 검정결과가 달라진다는 문제가 발생합니다.
이렇나 문제점을 보완하고자 p값(p-value)을 이용하는데, 이는 표본의 결과를 검정과정에 반영하는 방법입니다. 따라서 p값은 검정 과정에서 밝혀진(나타난) 유의수준이라고 볼 수 있습니다.
p.189~190
파이썬에서 일표본 t검정(one sample t-test)을 할 때 함수 scipy.stats.ttest_1samp()를 사용합니다.
| 함수 | 함수 인자 |
| scipy.stats.ttest_1samp(a, popmean, alternative) | - a : 배열 데이터 - popmean : 모집단 평균 - alternative = 'two-sided' = 'less' (one-sided) = 'greater' (one-sided) |
p.197
파이썬에서 독립인 두 표본에 대한 t검정에 사용하는 함수 ttest_ind()의 사용법은 다음과 같습니다.
| 함수 | 함수 인자 |
| scipy.stats.ttest_ind(a, b, equal_var, alternative) | - a, b : 배열 데이터 - equal_var : 'False' (분산이 같지 않을 경우) - alternative : 'two-sided' 'less' (one-sided) 'greater' (one-sided) |
두 표본의 분산이 같다는 가정(등분산 가정)을 나타내는 equal_var='True' 부분은 디폴트이므로 생략할 수 있으며, 두 분산이 같지 않다는 가정(equal_var='False')이라면 Welch의 t-test를 사용하여 검정합니다.
p.201
두 표본에 대한 t검정에 사용하는 함수 ttest_ind()를 사용하기 전에 두 집단의 분산이 같은지 또는 다른지를 검정하는 방법으로 Levene의 등분산 검정을 사용할 수 있습니다.
| 함수 | 함수 인자 | 결과 |
| scipy.stats.levene(a, b, center) | - a, b : 배열 데이터 - center = 'mean' = 'median' |
- statsitic : 검정통계량 - pvalue : p값 |
p.203
파이썬에서 독립인 두 표본에 대한 t검정에서 데이터가 없고 평균, 표준편차 등의 기술통계량만 알고 있는 경우에 사용하는 함수 tteset_ind_from_stats()의 사용법은 다음과 같습니다.
| 함수 | 함수 인자 |
| scipy.stats.ttest_ind_from_stats(mean1, std1, nobs1, mean2, std2, nobs2, equal_var, alternative) | - mean1, mean2 : 두 집단 평균 - std1, std2 : 두 집단 표준편차 - nobs1, nobs2 : 두 집단 사례 수 - equal_var = 'False' (이분산일경우) - alternative = 'two-sided' = 'less' (one-sided) = 'greater' (one-sided) |
p.204
초등학교 입학생을 대상으로 좌측과 우측의 시력에 차이가 있는지를 비교하거나 운동 전과 운동 후의 혈압에 차이가 있는지를 비교할 때 한 사람에 대해 두 개의 데이터가 짝을 이루게 되며, 두 개의 데이터는 동일한 사람에 의하여 만들어진 것이기에 서로 독립적이지 않습니다. 이러한 데이터를 대응 표본(matched sample 또는 paired sample)이라 합니다.
p.205
파이썬에서 대응 표본에 대한 t검정은 함수 ttest_rel()을 사용하며, 함수 인자는 다음과 같습니다.
| 함수 | 함수 인자 |
| scipy.stats.ttest_rel(a, b, alternative) | - a, b : 배열 데이터 - alternative : 'two-sided' 'less' (one-sided) 'greater' (one-sided) |
'Growth > 통계' 카테고리의 다른 글
| 스토리가 있는 통계학 (0) | 2023.02.03 |
|---|---|
| 맥주와 t분포 (0) | 2023.02.01 |
| Easy as ABC: A Quick Introduction to Bayesian A/B Testing in Python (Will Barker) (0) | 2022.12.27 |
| Talking Bayes to Business: A/B Testing Use Case | Shopify (0) | 2022.12.26 |
| Easy introduction to gaussian process regression (uncertainty models) (0) | 2022.12.04 |


댓글