p.7
근대의 통계학은 크게 영국, 독일, 프랑스 세 개의 국가에서 큰 발전을 일으켰다. 영국의 정치산술파 통계학은 창시자 존 그랜트를 따라 패티(W. Petty, 1623~1687)의 인구통계표, 핼리혜성으로 유명한 애드먼드 핼리(Edmond Halley, 1656~1742)의 보험수학과 생명표 등이 탄생했다. 핼리의 생명표는 예를 들어 '20세인 사람이 그 해에 사망할 확률은 100분의 1이고 50세인 사람은 39분의 1이다'라는 식으로 통계적으로 연령에 따른 사망 확률을 예측했다.
독일 대학파 통계학의 창시자인 콘링(H. Conring, 1606~1681)은 국정론을 통해 정치, 경제, 사회, 토지, 인구 등 국가 요소들을 통계적으로 정리하고 국가를 파악하고자 했고 아헨발(Achenwall Gottfried, 1719~1772)은 통계학(Statistik)이라는 용어를 처음으로 사용헀다. 그리고 프랑스에서는 순열과 조합으로 확률 계산의 기초를 마련한 베르누이(Daniel Bernoulli, 1700~1782)와 정규분포, 최소제곱법 등의 개념을 고안한 가우스(Carl Friedrich Gauss, 1777~1855) 그리고 확률론을 체계화한 라플라스(Pierre-Simon Laplace, 1749~1827) 등의 인물들을 통해 확률론을 발전시켰다.
p.15
최종 분석에는 전체 데이터를 사용하더라도, 분석 모델이 완성될 때까지는 표본 데이터를 활용하는 것이 경제적, 시간적으로 유리하다.
p.16
데이터 가공 및 변환이 수도 없이 일어나는 예측 및 분류 모델링 단계에서는 적절한 표본을 추출해서 진행하고 전체 프로세스가 완성됐을 때 전체의 데이터를 사용하여 최종적인 모델 성능을 확인하고 예측 및 분류를 하는 것이 좋다.
p.17
모집단과 표본은 자연적으로 차이가 존재한다. 1,000개의 관측치가 있는 모집단에서 999개를 추출한 표본이라 해도 그 평균과 분산은 약간의 차이가 날 것이다. 이러한 모집단과 표본의 자연 발생적인 변동을 표본 오차(sampling error)라 한다. 즉 같은 크기의 두 개의 표본을 주의해서 추출한다고 해도 완전히 동일한 표본을 얻는 것은 거의 불가능할 것이다. 표본오차는 추론통계의 개념을 이해하는 데 중요한 개념이다. 이를 제외한 변동을 비표본 오차(non-sampling error)라고 한다. 비표본 오차의 한 원인이 바로 편향(bias)이다. 편향은 표본에서 나타나는 모집단과의 체계적인 차이다.
p.32
구조방정식 모델은 "측정모형과 이론모형을 통해서 모형 간의 인과관계를 파악하는 방정식 모형"이라고 정의할 수 있다. 일반적으로 알고 있는 독립변수와 종속변수의 관계를 보다 복잡하게 구현하는 데 효과적인 분석방법이다.
독립변수와 종속변수가 다수 존재하여 종속변수 간의 관계까지 파악해야 하는 모델의 경우에는 단순한 회귀분석 모델은 각각의 모든 변수들 간의 유의치를 보지 못한다. 하지만 구조방정식은 독립-종속 변수 간은 물론 종속-종속 변수 간의 모든 유의치를 볼 수 있다. 이에 따라 구조방정식의 변수 개념도 약간은 고차원적이다. 독립변수와 종속변수의 개념은 관측변수(observed variable)와 잠재변수(latent variable)로 표현되고, 외생변수(exogeneous variable)와 내생변수(endogenous variable)의 개념으로도 확장이 가능하다.
관측변수(독립변수)들이 모여서 하나의 잠재변수(종속변수)를 설명하게 되고, 그 잠재변수가 다른 잠재변수와 관계를 갖게 되면서, 독립변수의 역할을 하는 외생변수가 되기도 하고 종속변수의 역할을 하는 내생변수가 되기도 한다. 이러한 관계는 외생잠재변수, 내생잠재변수, 외생관측변수, 내생관측변수로 표현되기도 한다.
p.49
결합확률(joint probability)은 표본공간 안에서 일어나는 사건 각각의 조합으로 이루어지는 확률이다. 즉 두 개 이상의 사건이 동시에 일어나는 확률을 뜻한다. 앞의 표에서 생산지가 수원인 동시에 A제품일 확률이 10%(P = 0.1)인 것과 같은 경우다. 결합확률은 P(A n B)로 표시하며, 사건의 교집합이라 볼 수 있다.
조건부확률(conditional probability)은 결합확률과 유사해 보이지만, 하나의 사건이 먼저 발생했다는 조건이 전제된 상황에서 또 다른 사건이 발생할 확률이라는 점에서 차이가 있다. 먼저 조건을 주어 표본공간을 한정 지은 다음, 다른 조건의 확률을 구하기 때문에 조건부 확률은 결합확률보다 확률 값이 높게 측정된다. 예를 들어 수원에서 생산하는 제품 중 C제품을 생산될 확률을 구한다고 했을 때, 수원에서 생산된 제품은 이미 발생했기 때문에 표본공간은 전체인 1,000이 아닌 수원 제품인 400이 된다. 그래서 C제품일 확률은 100/400, 즉 25%가 되는 것이다. 조건부확률은 동시에 발생하는 결합확률을 첫 번째 조건의 한계확률로 나눠 계산한다. 다시 말해 수원의 C 제품인 결합확률 0.1을 생산지가 수원이라는 한계확률 0.4로 나눠주면, 0.1 / 0.4 = 25%가 계산된다. 이는 P(B | A)로 표현하며, 이 중 A가 먼저 전제되는 조건을 의미한다.
p.51-52
당신은 제법 규모가 큰 커뮤니티 사이트를 운영하고 있다. 그런데 사이트 규모에 비해 배너광고 수익이 신통치 않다. 광고 클릭률(CTR)이 1%에 불과한 것이다. 그래서 수익을 어떻게 하면 늘릴 수 있을까 고민하던 중, 사이트에 평소 유입되는 남녀의 성비가 남성 80%, 여성 20%라는 정보를 알아냈다. 그래서 남성을 타깃으로 배너광고만 올리면 되겠다 싶었다. 그런데 또 고민이 생겼다. 알고 보니 남성의 광고 클릭률(CTR)은 0.5%인 반면, 여성의 광고 클릭률(CTR)은 무려 3%나 되는 것이었다. 이럴 경우, 어떤 성별을 타깃으로 배너광고를 올리는 것이 더 효과적일까?
이러한 상황에서 베이지안 이론을 활용하면 광고 전략의 방향을 간단하게 알아낼 수 있다. 먼저 배너광고를 클릭하는 사람 중 남성의 비율이 얼마나 되는지 알아보자.
P(남성 | 클릭) = (클릭 | 남성) * P(남성) / P(클릭률) = 0.005 * 0.8 / 0.01 = 0.4
남성의 클릭률과 남성의 확률을 곱해준 다음, 전체 클릭률인 0.01(1%)로 나누어 주었다. 결과는 40%가 나왔다. 나머지 60%는 여성인 것일까? 확인해보자.
P(여성 | 클릭) = (클릭 | 여성) * P(여성) / P(클릭률) = 0.03 * 0.2 / 0.01 = 0.6
계산 결과, 역시 여성이 60%로 나왔다. 따라서 비록 전체 유입 유저의 80%가 남성이지만, 광고를 클릭하는 유저는 여성이 더 많기 때문에(60%), 남성을 타깃으로 배너광고만 올리는 것은 올바른 전략이 아닌 것으로 판단된다. 이 예시는 이해를 돕기 위해 다소 과장이 있다. 그리고 상황이 단순하여 직관으로도 결과를 예상하는 것이 어느 정도 가능하다. 하지만 분류가 단순한 남녀가 아닌 10대 남성, 20대 남성... 60대 여성 등 복잡하게 나눠지면 베이지안 이론이 매우 유용하게 활용될 수 있다.
p.60-61
초기하분포(hypergeometric distribution)는 이항분포(베르누이 시행)와 달리, 각 시행이 서로 독립적이지 않아서 시행마다 성공할 확률이 달라진다. 왜냐하면 이항분포는 복원추출이지만 초기하분포는 비복원추출이기 때문이다. 복원추출은 표본에서 하나를 추출하고선 다시 표본에 포함시키고 추출하는 방법이다. 그렇기 때문에 매 추출마다 처음의 표본이 그대로 적용된다. 하지만 비복원추출은 한 번 추출하면 다시 채워넣지 않기 때문에 앞서 추출된 관측치를 제외하고 확률을 계산한다.
예를 들어 남성 2명과 여성 8명으로 이루어진 총 10명의 집단에서 처음에 남성 한 명을 뽑으면 다음에 남성이 뽑힐 확률은 복원 추출의 경우 그대로 2/10이지만, 비복원 추출은 1/9이 되는 것이다.
이를 응용하여 좀 더 복잡한 경우에 대입해 보자. A팀 10명, B팀 40명, C팀 50명으로 이루어진 한 회사에서 임의로 10명을 비복원추출로 뽑았을 때 A팀에서 2명이 뽑힐 확률은 어떻게 구할 수 있을까? 우선 전체 100명 중에서 10명을 뽑는 경우의 수는 100 combination 10으로 구할 수 있다. 이 100C10이 분모가 되고 분자는 뽑힌 10명 중 2명은 A팀이고 나머지 8명은 그 외의 팀이 되는 경우의 수가 되어야 한다. 따라서 확률을 수식으로 나타내면 다음과 같다.
10C2 * 90C8 / 100C10
이를 계산하면 A팀에서 2명이 뽑힐 확률은 약 0.4%이다.
p.66-68
지수분포(exponential distribution)는 특정 사건이 발생한 시점으로부터 다음 사건이 발생할 때까지의 시간을 확률변숫값으로 하는 분포를 뜻한다.
앞의 이산확률분포에서 다뤘던 포아송분포가 특정 사건이 발생하는 횟수를 나타내는 변수였다면, 지수분포는 발생하는 사건 다음 사건이 일어날 때 대기 시간을 다룬다는 것에 차이가 있다. 길이나 무게는 무한히 쪼갤 수 있듯이, 시간도 특정 구간에 무한한 변숫값이 존재할 수 있으므로 시간을 나타내는 지수분포는 연속확률분포다. 예를 들어 A 가전업체의 A/S 센터에 전화가 걸려온 후 다음 전화가 걸려올 때까지의 시간에 대한 확률변수를 그래프로 나타내면 다음과 같은 형태가 될 것이다.

지수분포 그래프에서 알 수 있듯이, 확률변수 X인 시간이 증가할수록 사건이 발생할 확률이 지수적으로 감소하고 있다. 오랜 시간이 지날수록 전화가 한 번도 걸려오지 않을 확률은 매우 적어진다는 의미다. 지수분포는 표준정규분포처럼 절대적인 기준이 없고 평균에 따라 기울기가 정해진다. 지수분포는 포아송분포와 밀접하게 연관되어 있으므로, 포아송분포의 확률밀도함수 기호인 람다(lambda)를 사용한다.
지수분포의 확률밀도 함수는 f(x) = λe^(-λx)로 나타낸다.
- x : 사건과 다음 사건 사이의 시간의 확률변수
- e : 자연로그의 밑
- λ : 특정 시공간 안에서의 평균 사건 발생 횟수
포아송분포에서 일정 시간동안 평균적으로 발생하는 사건의 횟수를 뜻했던 λ에 역수를 취하면 하나의 사건이 발생한 후, 다음 사건이 발생하기까지의 평균 소요시간이 된다. 평균을 제곱하면 분산이 되며, 분산에 제곱근을 취한 값인 표준편차는 평균과 동일하다. 이를 정리하면 다음과 같다.
- 지수분포의 (소요시간) 평균 : mu = 1 / λ
- 지수분포의 (소요시간) 분산 : sigma^2 = 1/ λ^2
- 지수분포의 (소요시간) 표준편차 : sigma = sqrt(1/ λ^2)
그렇다면 지수분포상의 실제 확률을 구하려면 어떻게 해야 할까? 우선 확률 분포의 경우를 3가지로 나누어 상황에 맞게 적용해야 한다.
1. t시점 이전에 발생할 확률 ( 1- e^(-λx))
2. t시점 이후에 발생할 확률 ( e^(-λx))
3. t시점과 t'시점 사이에 발생할 확률 (-e^(-λx)) - (-e^(-λx))
예를 들어 A 가전업체의 A/S 센터에 1시간당 평균 5회의 전화가 걸려온다면, 전화 간의 평균 시간 간격은 0.2시간이 된다. 이는 λ = 5이고, 1/ λ = 1/5 = 0.2으로 정리할 수 있다. 즉 포아송분포의 평균 λ은 5이며, 지수분포의 평균은 0.2가 되는 것이다. 이러한 조건에서 전화가 걸려온 후, 30분 이내에 전화가 올 확률은 1 - e^(-5 * 0.5) = 1 - 0.08208 = 0.918으로 계산할 수 있다. 다시 말해 91.8%의 확률로 전화 후에 30분 안에 또 전화가 올 것이라 해석할 수 있다.
p.77
유의수준과 반대되는 기준이 신뢰수준(Confidence Level)이다. 예를 들어 모평균(mu)을 추정하기 위해 100번의 실험(샘플링)을 수행했다고 해보자 실험을 통해 얻은 100개의 표본 평균과 표본 분산이 있을 것이다. 이때 유의수준을 0.05로 설정했다면, 100번의 실험 중 귀무가설이 참임에도 불구하고 귀무가설을 기각하는 오류의 최대 허용 한계를 5번으로 한다는 뜻이다. 유의수준이 0.05면 신뢰수준은 0.95가 된다. 유의수준과 신뢰수준을 합하면 100%가 된다.
p.79
일반저거으로 유의수준(alpha)는 0.05, 1 - 검정력(beta)은 0.2 기준을 사용하며, 1종 오류를 2종 오류보다 더 중요하게 생각한다. 1종 오류는 기존의 명제인 귀무가설을 잘못 판단하기 때문에 문제가 더 커질 수 있다. 예를 들어 혈압 개선 약품을 테스트한다고 했을 때, 실제로는 이 약이 효과가 없음에도 효과가 있는 것으로 잘못 판단했다면, 개발한 약품 회사는 큰 손해를 입게 될 것이다. 나중에 효과가 없는 것으로 밝혀져 법적 책임을 물게 될 수도 있고, 개발하고 생산한 제품을 모두 폐기해야 하기 때문이다.
p.88
p.91-92
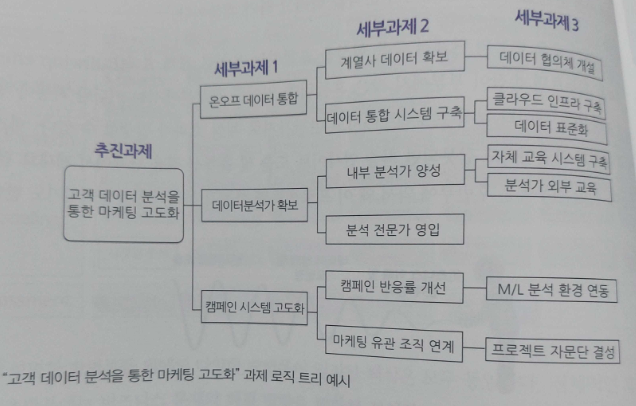
분석 프로젝트는 데이터 탐색을 하기 전까지 데이터에 숨겨져 있는 정보와 인사이트를 확인하기가 어렵다. 그래서 분석 목적을 설정하기 전에 PoC나 간단한 샘플 데이터 탐색 과정을 거치면 좋겠지만, 그러한 여건 주어지지 않는 경우가 많다. 따라서 분석 프로젝트의 방향이 언제든 바뀔 수 있다는 것을 염두에 두어야 한다.
기존의 명확했던 분석 목적이 무의미해지고 '무엇을 하려 하는가?'에서 '이 데이터로 우리가 할 수 있는 것은 무엇인가?'로 콘셉트가 변하는 경우가 발생하기도 한다. 이런 일은 자연스러운 상황이기 때문에 자신의 실력이 부족하다고 자책하거나 데이터가 부족하다고 불평할 필요는 없다. 중요한 것은 이렇게 콘셉트가 바뀌는 순간을 확실히 인지하고 신속하게 모든 팀원과 실무자들과 공유해야 한다. 그렇지 않을 경우 프로젝트가 어느 정도 진행됐을 때 프로젝트의 목적이 불확실해져 혼란이 발생할 수 있다. 심한 경우 프로젝트 기간 막바지에 도출된 결과를 실무진이나 경영진이 받아들이지 않아 프로젝트가 큰 위험에 닥칠 수 있다.
필자의 경험을 통한 한 가지 사례를 예로 들자면, 특수 원사를 생산하는 공정에서 원재료를 정제해주는 필터의 적정 교체시기를 예측하는 모델을 구축하는 프로젝트를 진행한 적이 있었다. 필터의 수명이 다하게 되면 원사를 타래에 감는 중에 절사가 자주 발생하게 된다. 절사가 발생하게 되면 제품 불량에 따른 손실이 발생되고 공정이 중지됨에 따라 생산성이 악화된다. 그렇기 때문에 필터 수명이 다 하기 전에 미리 대비하기 위해서 프로젝트가 시작됐다. 그런데 막상 필터 교체 이력 공정의 센싱 데이터를 분석해보니, 필터 교체와 절사 발생률 간의 관계를 찾아낼 수가 없었다. 적어도 데이터상으로는 절사 발생과 필터 수명은 상관이 없었던 것이다.
이에 따라 우리는 분석 목적을 신속히 전환해야만 했다. 우선 데이터 탐색과 시각화를 통해 데이터의 특성을 파악하고 실무자와의 집중적인 회의를 통해 현 상황의 문제점을 공유하고 해결 방안을 모색했다. 필터의 교체 시기 예측은 힘들게 됐지만, 당시 공정의 1차적인 문제점은 절사가 발생하는 것은 확실했다. 따라서 공정의 온도, 회전 속도, 압력 등의 센서 데이터를 통해 절사와 관련성이 높은 요소를 찾고 이를 활용하여 절사율을 낮출 수 있도록 프로젝트 목저거을 성공적으로 전환할 수 있었다. 결국 필터 교환 시기 예측 프로젝트는 원사의 절사 개선 프로젝트로 바뀌었고, 유의미한 결론을 도출하여 성공적으로 프로젝트를 마칠 수 있었다.
p.104-105
데이터 분석가는 기본적으로 데이터 분석 역량뿐만 아니라 데이터베이스 서버 환경에 대해서도 어느 정도는 알고 있어야 한다. 그래야 효율적으로 데이터를 끌어오고 가공하여 분석할 수 있다. 일반적으로 전체적인 데이터 흐름은 OLTP -> DW(ODS) -> DM -> OLAP으로 이루어진다. 이러한 흐름은 데이터라는 제품이 생산되고, 창고에 저장했다가 소매점으로 옮겨진 후 최종적으로 소비자가 데이터를 갖게 되는 과정이라고 생각하면 된다.
OLTP(Online Transaction Processing)는 실시간으로 데이터를 트랜잭션 단위로 수집, 분류, 저장하는 시스템이다. 예를 들어 숨낳은 입출금이 일어나는 은행에서 기록을 오류 없이 실시간을 처리하고 저장하는 시스템이라고 할 수 있다. 이처럼 데이터가 생성되고 저장되는 처음 단계가 OLTP다.
DW(Data Warehouse)는 말 그대로 데이터 창고와 같은 개념이다. 수집된 데이터를 사용자 관점에서 주제별로 통합하여 쉽게 원하는 데이터를 빼낼 수 있도록 저장해놓은 통합 데이터베이스다. 여러 시스템에 산재되어 있던 데이터들을 한 곳으로 취합하여 모아놓는 저장소다. DW를 통해 OLTP를 보호하고 데이터 활용 훃율을 높일 수 있다. DW와 비슷한 개념으로 ODS(Operational Data Store)가 있다. ODS는 데이터를 DW에 저장하기 전에 임시로 데이터를 보관하는 중간 단계의 저장소라 할 수 있다. DW가 전체 히스토리 데이터를 보관하는 반면 ODS는 최신 데이터를 반영하는 것에 목적이 있다.
DM(Data Mart)는 사용자의 목적에 맞도록 가공된 일부의 데이터가 저장되는 곳이다. 기업의 경우 마케팅 팀, 인사 팀, 총무 팀 등에서 필요한 데이터는 서로 다를 것이다. 이처럼 부서나 사용자 집단의 필요에 맞도록 가공된 개별 데이터 저장소가 DM이다. 이를 통해 접근성과 데이터 분석의 효율성을 높일 수 있으며, DW의 시스템 부하를 감소시킬 수 있다.
p.107-108
맵리듀스는 크게 맵(Map)과 리듀스(Reduce)라는 두 단계로 구성된다. 맵 단계는 흩어져 있는 데이터를 관련된 데이터끼리 묶어서 임시의 집합을 만드는 과정이다. 그리고 리듀스 단계에서는 필터링과 정렬을 거쳐 데이터를 뽑아낸다. 맵리듀스의 중요한 특징은 key-value 쌍으로 데이터를 처리한다는 것이다. 예를 들어 자동차라는 key는 car라는 value를 갖고 맥주라는 key는 beer라는 value를 갖는 조합을 생각해보자. 맵 단계에서는 이렇게 '자동차-car', '맥주-beer'라는 각자의 쌍으로 레코드의 개념을 갖게 된다.
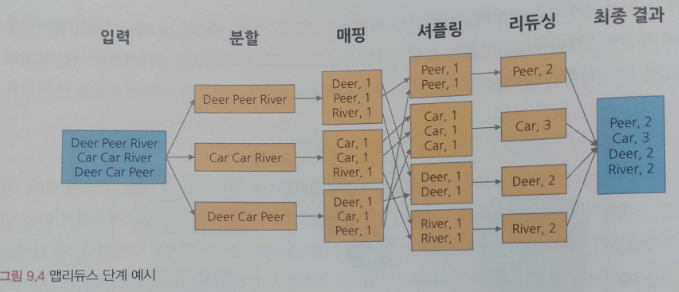
그리고 정렬과 병합 등의 과정을 통해 리듀스 단계에서 나눠져 있던 결과들을 취합하여 최종 결과를 생성한다. 다음의 word counting 예시를 통해 맵리듀스의 세부 단계를 확인해보자.
deer, beer, river 등으로 구성된 데이터에서 각 단어의 총 개수를 세고자 한다. 맵리듀스는 다음의 네 단계를 거쳐 단어의 수를 센다.
- 분할(spliting) : 입력된 데이터를 고정된 크기의 조각으로 분할한다.
- 매핑(mapping) : 분할된 데이터를 key-value 형태로 묶어주고 단어 개수를 계산한다.
- 셔플링(shuffling) : 매핑 단계의 counting 결과를 정렬 및 병합한다.
- 리듀싱(reducing) : 각 겨려과를 취합 및 계산하여 최종 결괏값을 산출한다.
p.123
EDA를 하는 가장 간단하면서 효과적인 방법은 각 데이터 샘플을 1,000개씩 뽑아서 엑셀에 붙여놓고 변수와 설명 리스트와 함께 눈으로 쭉 살펴보는 것이다. 그렇게 하면 빠른 시간 안에 데이터에 대한 전체적인 감을 잡을 수 있다. 예를 들어 고객 데이터가 있다면 단순 임의추출을 통해 1,000개의 행을 추출하여 변수 저어의를 확인한 다음 변수 하나하나 씩 눈으로 쭉 읽어보는 것이다.
'Growth > 통계' 카테고리의 다른 글
| 파이썬을 이용한 경제 및 금융데이터 분석 (0) | 2023.03.18 |
|---|---|
| 고급확률론 3월7일 (0) | 2023.03.08 |
| 스토리가 있는 통계학 (0) | 2023.02.03 |
| 맥주와 t분포 (0) | 2023.02.01 |
| 생활 속의 통계학 (0) | 2023.01.24 |

댓글