p.35
문제는 X와 Y의 상관관계가 밝혀져도 그것만으로는 인과관계가 있다고 말할 수 없다는 점이다. 상관관계와 인과관계가 다르다는 말에 다소 당황스러운 독자도 있을 것이다. 그런 사람을 위해 X와 Y에 상관관계가 있을 경우 어떤 가능성이 있는지 알아보았다.
1) X가 Y에 영향을 주었을 가능성
2) Y가 X에 영향을 주었을 가능성
3) V가 X와 Y 양쪽에 영향을 주었을 가능성
아이스크림 사례에서 다음 세 가지 가능성 중 어느 것이 진짜인지 판단할 수 없다
1) 광고(X)가 매출(Y)에 영향을 주었을 가능성
2) 매출(Y)이 광고(X)에 영향을 주었을 가능성
3) 다른 요인(V)이 광고(X)와 매출(Y) 양쪽에 영향을 주었을 가능성
p.44
통상적으로 데이터 관측수가 늘어나면 장점이 많다. 그러나 안타깝게도 데이터 관측수가 아무리 늘어나도 편향 문제는 해결되지 않는다는 사실이 수학적으로 증명되었다. 그래서 빅데이터가 모든 것을 해결해준다는 주장은 적어도 인과관계 분석에는 들어맞지 않는다.
p.51-52
개입효과를 활용해 인과관계를 정의하면 두 가지가 명확해진다.
첫째, 인과관계는 'A의 개입을 받았을 때의 결과(Y_1)'와 '개입을 받지 않았을 때의 결과(Y_0)'의 차이로 정의해야 한다.
둘째, A의 데이터로만 인과관계를 계산하는 것은 불가능하다. 2012년 여름 A는 가격 인상이라는 개입을 받았다. 덕분에 Y_1의 데이터가 관측 가능해졌다. 그러나 개입을 받지 않았을 때의 결과(Y_0) 데이터는 존재하지 않는다. 따라서 Y_1과 Y_0의 차이를 계산하는 것은 불가능하다. 반대로 A가 실제로 개입을 받지 않았다면 어떨까? 이 경우에는 개입을 받지 않았을 때의 결과(Y_0)는 관측할 수 있지만 개입을 받았을 때의 결과(Y_1)는 관측할 수 없게 된다.
이렇게 관측이 불가능한 결과를 '실제로는 일어나지 않은 잠재적 결과(counterfactual potential outcome)'라고 한다. 다시 말해 잠재적으로는 존재할 수 있지만 실제로는 일어나지 않았으므로 현실에서는 관측 불가능한 데이터라는 의미다. 사실에 반하는 결과라는 의미로 '반사실의 잠재적 결과' 혹은 '반실가상적 사실'이라고 부르기도 한다. 한자어가 나열되어 다소 어려우므로 여기서는 '실제로는 일어나지 않은 잠재적 결과'로 쓰기로 한다.
특정 시기에 한 개인에게서는 Y_1이나 Y_0 중 하나만 관측할 수 있고 다른 하나는 관측할 수 없다. 그래서 한 개인의 데이터에서 Y_1과 Y_0의 차이를 계산해 인과관계를 측정하는 것은 근본적으로 불가능하다. 이것을 '인과적 추론의 근본 문제'라고 부른다(Holland, 1986).
p.59-63
왜 무작위로 집단을 나누는 것이 중요할까? 예를 들어 200명의 소비자를 무작위로 나눈다고 하자. 200명이 똑같이 나뉠 필요는 없지만 임의로 개입집단에 100명, 비교집단에 100명이 배정되었다고 하자.
무작위로 집단이 나뉠경우 어느 정도 표본 수가 확보되면 두 집단은 통계적으로 동질의 집단이 된다. 예를 들어 각 집단이 소유한 에어컨을 생각해보자. 만약 자기 선택에 따라 집단을 나누었다면 어떤 일이 일어날까? 전력 가격을 인상할지 말지를 소비자의 선택에 맡기면 '에어컨을 많이 소유한 소비자일수록 개입을 받기 싫다'고 생각할 것이다. 따라서 개입집단이 비교집단보다 에어컨을 적게 소유했을 가능성이 높다. 즉 개입집단과 비교집단 사이에는 '개입을 받는다'는 것 외에도 '소유한 에어컨 대수'에서도 차이가 생긴다.
그러나 집단을 무작위로 나누는 경우 이런 일은 일어나지 않는다. 주사위를 굴려서 홀수가 나온 소비자는 개입집단에, 짝수가 나온 소비자는 비교집단에 배정함으로써 이론적으로는 '두 집단이 소유한 에어컨 대수는 동등해진다'
따라서 집단이 무작위로 나뉘면 에어컨을 적게 소유한 소비자만 개입집단에 모이는 일은 벌어지지 않는다. 앞서 '이론적으로는'이라는 조건을 붙인 이유는 실제로 두 집단이 동질적인지를 관측하려면 어느 정도의 표본수가 확보되어야 하기 때문이다.
무작위로 집단을 나눌 경우 가장 큰 강점은 '에어컨 대수'라는 특정한 요인만이 아니라 온갖 요인에도 집단 간의 동질성이 확보된다는 점이다. 이를테면 두 집단은 소득, 집의 넓이, 가족 구성 같은 요인도 같아진다. 또 절전 의욕처럼 관측이 불가능한 요인도 동등해진다. 그렇기 때문에 무작위로 집단을 나눌 경우에는 '개입이 없었다면 비교집단의 평균적 결과(Y_c)와 개입집단의 평균적 결과(Y_T)가 같아진다'는 가정이 성립한다.
p.86
RCT 전문가인 시로커가 오바마 캠프에서 실시한 실험에서는 앞의 세 가지 원칙이 잘 지켜졌다.
1) 비교집단을 포함해 24개의 적절한 집단이 만들어졌고
2) 집단이 무작위로 나뉘었으며
3) 각 집단에 충분한 표본수가 채워졌다. 그러면 실험 결과는 어땠을까?
p.87
오바마 캠프의 RCT 결과
| 시작페이지 화면 시안 |
버튼 | 평균 등록률 (퍼센트) |
비교집단과의 차이(pp) | 표본수(명) | |
| 1위 | B | 더 알아보기 | 11.6 | +3.34 | 1만 2,947 |
| 2위 | C | 더 알아보기 | 10.3 | +2.04 | 1만 3,073 |
| 3위 | A | 더 알아보기 | 9.80 | +1.54 | 1만 3,025 |
| 비교집단 | A | 등록하세요 | 8.26 | - | 1만 3,167 |
p.103
RD디자인의 키워드는 불연속(discontinuity)과 경계선(borderline)이다.
p.110
RD디자인의 가정
- 만약 경계선에서 본인부담금(X)이 변화하지 않는다면 의료 서비스 이용자 수(Y)도 점프하지 않는다.
p.111~112
RD디자인의 가정은 '가상의'데이터에 기초하므로 데이터로 입증하는 것은 불가능하다. 분석자는 '아마 이 가정이 성립할 것'이라는 주장만 펼칠 수 있을 뿐이다.
이것이 자연실험과 RCT의 차이점이다. RCT에서는 무작위로 집단을 나누기만 하면 인과관계를 분석하기 위한 가정이 수학적으로 증명되었다. 하지만 RD디자인을 비롯한 자연실험 기법으로는 가정의 성립 여부를 수학적으로 증명하지 못하고 다만 가능성을 쌓아갈 수만 있다.
p.114~115
70세를 기준으로 본인부담금 이외의 무언가가 비연속적으로 변화하여 의료 서비스 이용에 영향을 미친다면 RD디자인의 가정도 무너진다. 예를 들어 70세 생일을 경계로 연금 지급액이 크게 인상된다면 어떨까(실제로 그런 일은 없다). 이 경우 RD디자인의 가정이 무너질 가능성이 있다. 왜 그럴까?
연금을 많이 받게 되면 그만큼 소득이 늘어나 의료 서비스에 사용할 자금이 생긴다. 다시 말해 연금 지급액 인상으로 의료 서비스 이용이 늘어날 가능성이 있다. 그렇다면 70세를 경계로 본인부담금이 바뀌지 않더라도 의료 서비스 이용이 비연속적으로 증가할(점프할) 가능성이 있으므로 RD디자인의 가정은 무너진다.
실제로 이런 일이 일어나면 관측된 환자 수의 점프는 70세 이후 연금 지급액이 인상된 영향이지, 본인부담금이 변화한 영향은 아니라는 비판이 성립한다. 그러면 RD디자인으로 측정된 효과가 본인부담금의 변화에 의한 것이라고 단언할 수 없게 된다.
RD디자인의 가정은 언제 또 무너질까? 바로 분석의 대상이 그래프 가로축의 변수를 조작할 수 있을 때다. 여기서는 환자가 자신의 나이를 속이는 경우다(물론 현실적으로는 불가능에 가깝다).
나이를 속이는 것이 가능할 경우 병약한 사람이나 소득이 낮은 사람 등이 자신의 나이를 70세 이상이라고 속일 가능성이 있다. 그렇게 되면 그래프에서 70세를 기준으로 오른쪽에는 원래 병약했던 사람이 모이고 왼쪽에는 비교적 건강한 사람이 모이게 된다. 이것은 70세를 경계로 의료비 본인부담금이 급격히 변화해서만이 아니라 병약한 사람이 나이를 속인 영향도 있는 것이다. 따라서 RD디자인에는 '분석 대상이 그래프 가로축의 변수를 자의적으로 조정할 수 없다'는 조건이 필요하다.
p.140
집군분석에는 다음과 같은 가정이 필요하다.
- 만약 연비 규제치(X)가 계단식으로 바뀌지 않는다면 자동차 무게(Y)의 분포는 점선처럼 매끈하고(연속적이고) 집적하지 않는다.
p.161
패널 데이터 분석에는 평형 트렌드 가정(parallel trend assumption)이 필요하다.
- 만약 개입이 일어나지 않았다면 개입집단의 평균값(Y_T)과 비교집단의 평균값(Y_C)은 평행한 추이를 보인다 (평행 트렌드 가정)
p.164-165
평행 트렌드 가정이 무너지는 다른 사례를 생각해보자. 아이스크림 신규 광고(X)와 매출(Y)을 예로 들어보자. 어느 해, 아이스크림 회사가 도쿄에서는 신규 광고를 하고 오사카에서는 하지 않았다고 하자. 이렇게 두 지역 간에 광고 집행 여부를 다르게 하면 도쿄를 개입집단으로, 오사카를 비교집단으로 하는 패널 데이터 분석이 가능할 듯 하다.
이때는 만약 도쿄에서 신규 광고를 하지 않았다면 도쿄와 오사카의 아이스크림 판매 추이는 평행하게 움직였을 것이라는 평행 트렌드 가정이 필요하다. 가령 이 아이스크림 회사가 신규 광고와 동시에 도쿄에서만 가격을 인하했다고 하자. 그러면 평행 트렌드 가정은 거의 틀림없이 무너진다. 가격 인하의 영향으로 도쿄와 오사카의 아이스크림 판매 추이는 평행이 되지 않기 때문이다.
또 신규 광고 이후 도쿄에만 무더위가 닥쳤다면 어떨까? 이것도 평행 트렌드 가정을 무너뜨린다.
신규 광고를 내보낸 후에 전국에 무더위가 닥쳤다면 어떨까? 이때 '무더위가 아이스크림 판매에 미치는 영향은 전국적으로 동일하다'는 가정이 성립하면 괜찮다. 앞서 이야기했듯이 이것은 두 집단에 함께 닥친 공통 쇼크다. 공통 쇼크는 평행 트렌드 가정을 무너뜨리지 않는다.
p.171
- 패널 데이터 분석을 이용하려면 복수의 집단에 대해 복수의 기간에 걸쳐 데이터를 수집할 수 있어야 한다.
- 패널 데이터 분석의 원칙
1. 개입을 전후해서 개입집단과 비교집단 양쪽의 데이터를 입수할 수 있는지 확인
2. 평행 트렌드 가정이 성립하는지 검증
3. 평행 트렌드 가정이 성립할 가능성이 높다면 두 집단의 평균값 추이를 그래프로 그림으로써 개입 효과의 평균값을 측정
- 패턴 데이터 분석의 강점
1. 필요한 데이터만 확보된다면 RD디자인이나 집군분석 이상으로 광범위하게 이용할 수 있다.
2. 결과를 그래프로 보여줄 수 있어 쉽고 투명한 분석이 가능하다.
3. 개입집단 전체에 대한 개입 효과를 분석할 수 있다. 분석 대상이 제한된 RD디자인이나 집군분석에 비해 강점이다.
- 패널 데이터 분석의 약점
1. 분석에 필요한 가정이 성립할 것이라는 근거를 제시할 수는 있지만 입증할 수는 없다. 이는 RCT와 비교했을 때 큰 약점이다.
2. RD디자인이나 집군분석에 필요한 가정에 비해 평행 트렌드 가정은 매우 까다로운 가정이며 실제로는 성립하지 않는 경우도 있다.
p.185-186
스탠퍼드대학의 라즈 체티 연구팀은 답을 얻기 위해 대형 슈퍼마켓과 협력하여 RCT를 실시했다(Chetty, Looney and Kroft, 2009). 이 실험은 실험실이 아니라 실제 슈퍼마켓에서 실시되었다는 점에서 매우 혁신적이었다.
먼저 표본으로 뽑힌 점포를 무작위 개입집단과 비교집단으로 나누었다. 또 개입집단에 판매되는 상품 중에 무작위로 뽑힌 상품군에만 세금이 포함된 가격을 표시했다. RCT 결과 다음과 같은 인과관계가 밝혀졌다.
- 세금이 포함된 가격을 표시하면 세금이 제외된 가격을 표시했을 때보다 매출이 평균 8퍼센트 하락한다
여기서 다시 강조하면 세금이 포함된 가격을 표시하든 세금이 제외된 가격을 표시하든 최종적으로 소비자가 계산대에서 지불하는 금액은 똑같다. 그런데도 세금이 포함된 가격을 표시했더니 매출이 8퍼센트나 떨어진 것이다.
흥미롭게도 당시 캘리포니아주의 소비세는 7.375퍼센트였다.
실험 결과 나타난 8퍼센트의 효과는 다음과 같이 해석할 수 있다. 즉 세금을 제외한 가격만 표시되었을 경우 소비자는 소비세를 거의 무시하고 상품 가격을 계산했다. 그래서 세금이 포함된 가격이 표시되자마자 세금만큼 가격이 오른 것처럼 소비행동을 바꾸었다.
p.194-197
우버는 운전자 수와 이용자 수를 실시간으로 확인함으로써 '수급핍박지수(surge generator)'를 계산한다. 이 지수가 클수록 거리에 나와 있는 운전자 수에 비해 이용자 수가 많다. 즉 수요가 공급을 초과하여 수급이 핍박한 상태다. 우버는 이 지수를 활용하여 다음과 같이 가격을 바꾼다.
1) 핍박지수가 1.15보다 크고 1.25보다 작을 때는 가격을 1.2배로 한다.
2) 핍박지수가 1.25보다 크고 1.35보다 작을 때는 가격을 1.3배로 한다.
핍박지수가 1.25를 넘지 않을 때의 가격은 1.2배다. 그러다 핍박지수가 1.25라는 경계점을 넘자마자 가격은 1.3배로 오른다.
그러면 이 상황에서 어떤 자연실험 기법을 이용할 수 있을까? 시카고대학 연구팀은 핍박지수를 잘 활용하면 RD디자인이 가능할지 모른다고 생각했다.
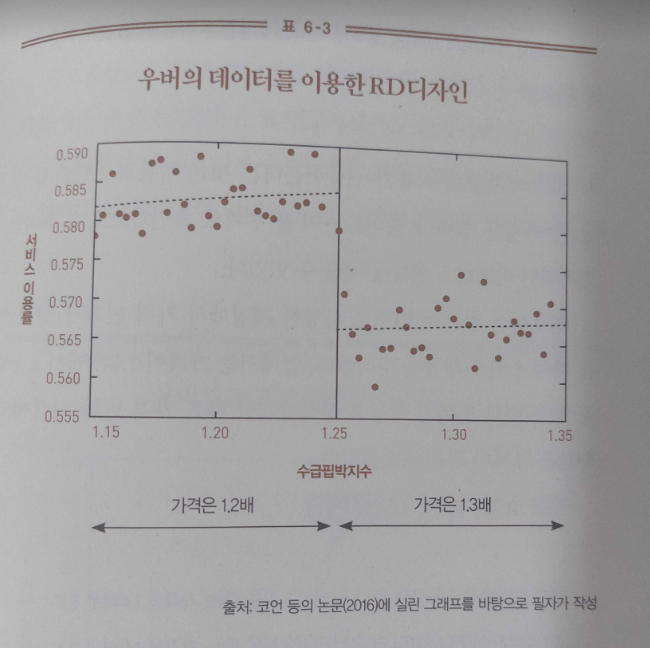
분석 결과의 일부가 요약되어 있다. 가로축은 수급핍박지수를 나타낸다. 세로축은 우버 택시를 부르려고 했던 소비자 가운데 스마트폰에 가격이 표시된 이후 실제로 운전자를 부른 소비자의 비율을 나타낸다. 예를 들어 세로축의 0.58이라는 숫자는 가격이 표시된 후에 58퍼센트의 소비자가 실제로 운전자를 부르고 나머지 42퍼센트는 운전자를 부르지 않았다는 뜻이다.
가격이 1.2배에서 1.3배로 바뀌는 순간 이용률이 비연속적으로 떨어진다. 3장에 소개된 RD디자인에 필요한 가정이 성립한다면 다음과 같은 인과관계를 보여줄 수 있다.
- 가격이 1.2배에서 1.3배로 오르면 서비스 이용률은 0.58에서 0.565로 떨어진다.
가격이 오르면 이용자가 줄어든다는 것은 직관적으로도 알 수 있다. 하지만 '얼마나 줄어드는지' 를 수치로 확인함으로써 우버는 효과적인 비즈니스 전략을 세울 수 있었다.
연구팀은 같은 방법으로 다양한 지점에서 가격 변화가 일어났을 때의 소비자 행동을 분석했다. 앞에서는 가격이 1.2배에서 1.3배로 오를 떄의 소비자 행동을 분석했지만 다른 가격 변화 지점에도 똑같은 규칙이 적용되고 있었다.
예를 들면 다음과 같은 식이다.
3) 핍박지수가 1.35보다 크고 1.45보다 작을 때는 가격을 1.4배로 한다.
4) 핍박지수가 1.45보다 크고 1.55보다 작을 때는 가격을 1.5배로 한다.
연구팀은 RD디자인을 이용하여 가격 상승과 하락에 따른 이용률 변화를 추정했다.
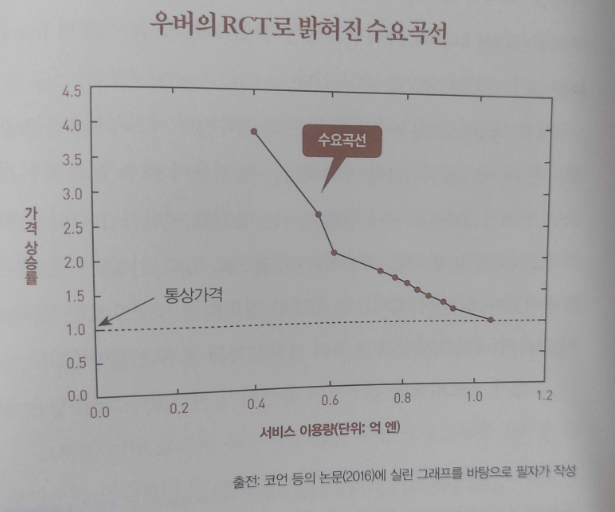
세로축은 가격을 나타낸다. 예를 들어 1.0은 통상가격이다. 따라서 1.5는 통상가격의 1.5배라는 의미다. 또 가로축은 소비량을 나타낸다. 즉 이 그래프는 경제학 교과서에 자주 나오는 수요곡선을 우버의 빅데이터를 활영하여 그린, 말하자면 사실적인 수요곡선이다.
p.210
| 분석 방법 | 외적 타당성의 범위 개입효과(인과관계)를 분석할 수 있는 대상 |
내적 타당성의 강도 |
| RCT(강제 참가형) | 실험 대상자 | 매우 높다 |
| RCT(자발적 참가형) | 실험 대상자 중 자발적 참가자 | 매우 높다 |
| RD디자인 | 경계선 부근의 대상 | 높다 |
| 집군분석 | 집적한 대상 | 높다 |
| 패널 데이터 분석 | 개입집단 전체 | 약간 떨어진다 |
'Growth > 통계' 카테고리의 다른 글
| 행동 데이터 분석 (0) | 2023.06.20 |
|---|---|
| 말로만 말고 숫자로 대봐 (0) | 2023.05.28 |
| 파이썬을 이용한 경제 및 금융데이터 분석 (0) | 2023.03.18 |
| 고급확률론 3월7일 (0) | 2023.03.08 |
| 데이터 분석가가 반드시 알아야 할 모든 것 (1) | 2023.02.04 |


댓글